GWR数据分析基本流程
2022年3月20日
编程
地理加权回归(Geographically Weighted Regression, GWR)技术将地理学第一定律深度融入局部空间统计方法,通过对独立抽样的分析点分别进行回归分析模型解算,得到与空间位置一一对应的空间回归系数,以随着空间位置不同而变化的参数估计量化表征空间关系异质性特征。
目前有很多软件可以进行地理加权回归分析,本文主要介绍使用 [**GWmodel**](https://cran.r-project.org/web/packages/GWmodel/index.html) 包的方式,构建 GWR 模型进行数据分析。
# 数据
本文所使用的数据是 **GWmodel** 包中所提供的 *londonhp* 数据,可以使用如下方式进行加载:
```R
data(LondonHP)
```
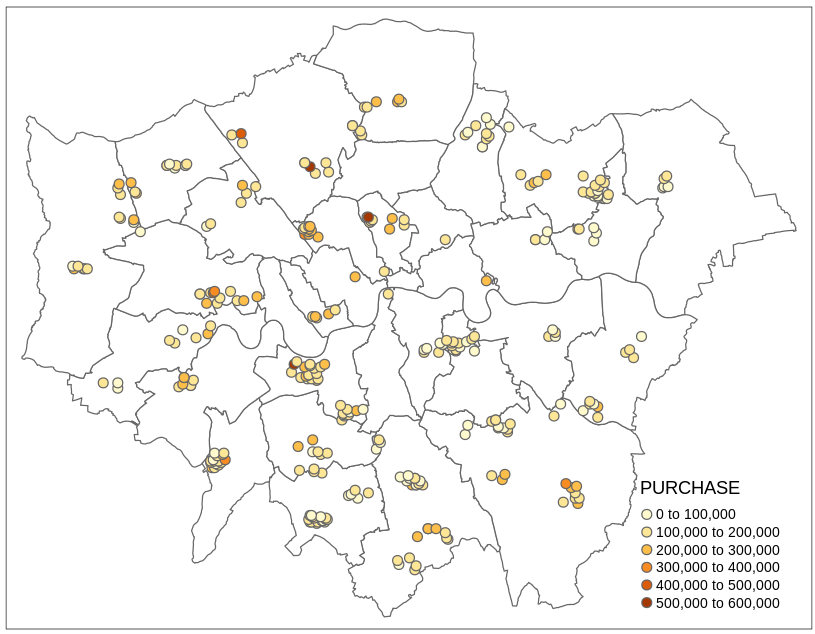
该数据中,将 `PURCHASE` 作为因变量,自变量主要取 `FLOORSZ` `BATH2` `UNEMPLOY` `PROF` 四个。
# 分析过程
地理加权回归分析一般情况下分为三步:模型优选、带宽优选、模型拟合。首先通过模型优选过程剔除无关变量以找到最优变量组合,然后使用贷款优选过程选出最优带宽,最后使用最优变量组合和最优带宽拟合地理加权模型。
> ***为了更清楚地展示函数使用方式,所有函数调用地参数都显式地指定其名字。***
## 模型优选
模型优选使用 `gwr.model.selection()` 函数,该函数根据指定的自变量、因变量执行前向选择法,并给出所有模型的变量组合以及 AIC 、AIC~c~ 等值。得到结果后,在通过 `gwr.model.sort()` 函数对模型进行排序。
```R
model.step <- gwr.model.selection(DeVar = "PURCHASE", InDeVars = c("FLOORSZ", "BATH2", "UNEMPLOY", "PROF"),
data = londonhp, adaptive = T, bw = Inf, kernel = "bisquare",
approach = "CV", longlat = F)
model.sort <- gwr.model.sort(Sorting.list = model.step, numVars = 4, ruler.vector = model.step[[2]][,2])
```
这段代码先调用 `gwr.model.selection()` 函数执行一个前向逐步回归的变量选择过程。带宽 `bw` 可以取任意数值,包括 `Inf` ,此时所有样本的权重都是 1。该函数中的参数主要有:
| 参数 | 取值 | 说明 |
| ------------ | ------------------- | ------------------------------------------------------- |
| `DeVar` | 字符串 | 因变量在数据中的列名 |
| `InDeVar` | 字符串向量 | 自变量在数据中的列名 |
| `data` | Spatial*DataFrame | 要分析的空间数据 |
| `adaptive` | 布尔值 | 为`True` 时表示带宽类型是可变带宽,否则表示是固定带宽 |
| `bw` | 数值 | 带宽值 |
| `kernel` | 字符串 | 权重核函数的名称,一般取`bisquare` 或 `gaussian` |
| `approach` | 字符串 | 模型优选的方法,一般取`CV` 或 `AIC` |
| `longlat` | 布尔值 | 指示数据中的坐标是否是经纬度 |
然后调用 `gwr.model.sort()` 函数对所有尝试过的模型进行排序,排序后才能判断究竟选择那个模型。该函数中的主要参数有:
| 参数 | 取值 | 说明 |
| ---------------- | -------- | ------------------------------------------------------------------ |
| `Sorting.list` | | 函数`gwr.model.selection()` 的返回值 |
| `numVars` | 整型值 | 自变量的数量 |
| `ruler.vector` | | 函数`gwr.model.selection()` 的返回值中第二项的以列,通常取第二列 |
这两个函数的返回结果 `model.step` 和 `model.sort` 是一个列表,由两部分组成:模型列表和模型指标。
* `model.step[[1]]` 是所有模型的列表,通过索引模型编号可以获取对应的模型,例如使用 `model.step[[1]][[99]]` 可以获取第 99 个模型,获取的结果依然是一个列表,第一个元素是模型表达式,第二个元素是所有自变量组成的向量。
* `model.step[[2]]` 是所有模型有关指标的表,每行是一个模型,共有 4 列,分别是:带宽、AIC、AICc、残差。
对于优选结果,我们通常使用可视化方法来分析应该选择哪个模型。通常会用到三个图:模型变量环形图、模型指标折线图、模型指标差分图。
### 模型变量环形图
该图展示了所有尝试过的模型所拥有的变量组合。
```R
gwr.model.view(DeVar, InDeVars, model.list)
```
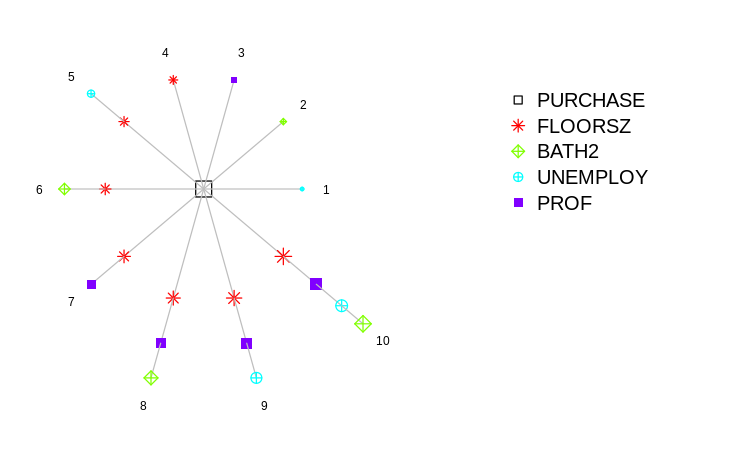
该图左侧是一个放射形环状结构,每一条放射线代表一个模型,线上的每一个符号代表一个变量。不同符号所代表的变量在右边图例中一一对应。
### 模型指标折线图
设向量 `ruler` 表示模型某个指标值(通常使用 AICc 值作为模型指标,即使用 `model.sort[[2]][,2]`),那么可以使用如下代码进行绘图。
```R
plot(ruler, col = "black", pch = 20, lty = 5, type = "b", ylab = "AICc")
for (i in 1:num.vars) {
abline(v = sum(num.vars:(num.vars - i + 1)), lty = 2)
}
```
![]()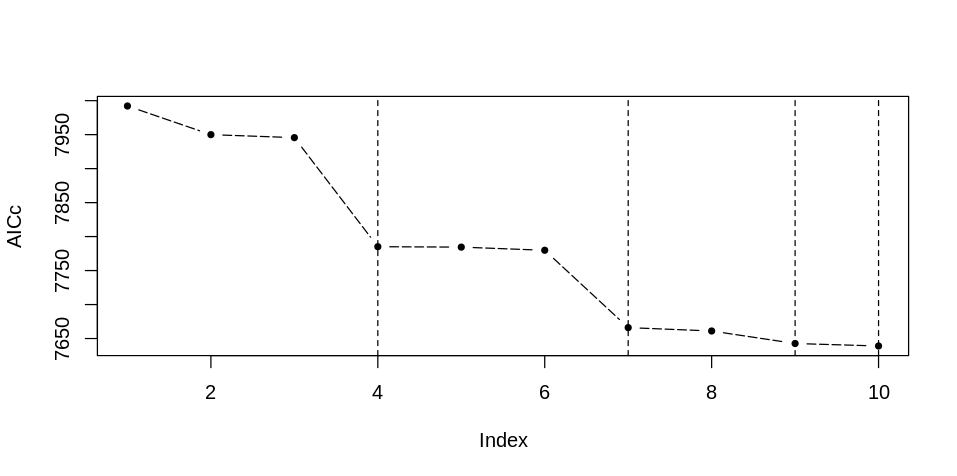
图中竖线表示从下一个模型开始,模型中变量总数+1。
根据前向选择法的理论:当一个模型与前一个模型相比 AICc 值下降超过某一阈值时(通常设该阈值为 3 )表示该模型所添加的变量对模型的拟合效果具有显著的改进。因此,找到最后一个 AICc 值下降超过阈值的模型,即可作为优选出的模型。得到该模型后,有两种获取模型变量组合的方法:
1. 根据模型编号,在模型变量环形图中找到对应的模型,读出模型的变量组合。
2. 根据模型编号 `model.best.id`,使用下列代码获取模型,之后通过 `model.best[[2]]` 模型自变量,通过 `formula(model.best[[1]])` 获取模型回归方程 `model.formula`。
```R
model.best <- model.sort[[1]][[model.best.id]]
model.best.formula <- formula(model.best[[1]])
```
### 模型指标差分图
该图与模型指标折线图相比更容易分析模型与前一模型相比时的改进度。同样对于模型指标值向量 `ruler`,可以使用下面的方法进行绘图,得到模型指标差分图。
```R
ruler.diff <- c(0, diff(ruler))
plot(ruler.diff, ylim = c(-50, 0))
abline(h = -3)
ruler.diff.show <- which(ruler.diff < -3 & ruler.diff > -50)
text(x = ruler.diff.show, y = ruler.diff[ruler.diff.show] - 1,
labels = as.character(ruler.diff.show))
for (i in 1:4) {
abline(v = sum(4:(4 - i + 1)), lty = 2)
}
```
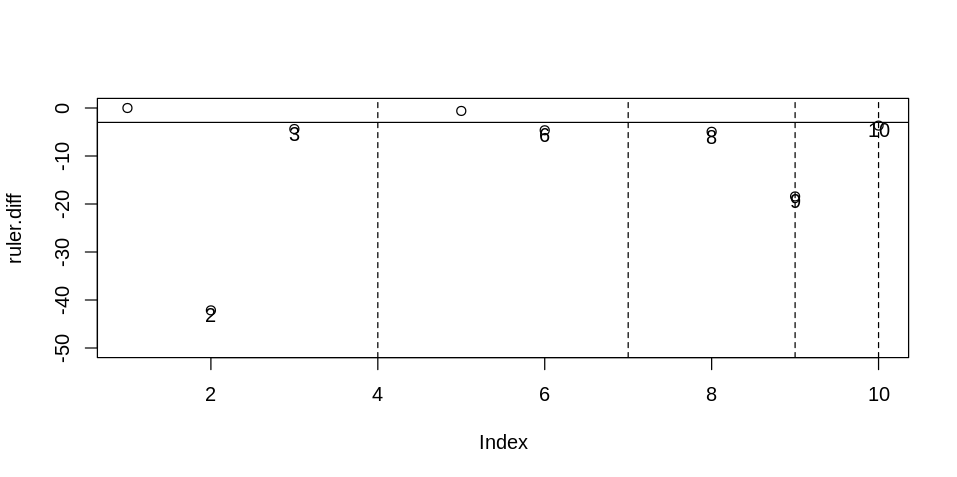
通过该图可以清晰地看到那些模型与上一个模型相比具有显著改进效果。在这里我们选择第9个模型作为最优模型。因为第10个模型与之相比,改进的幅度很小。也就是说,第9个模型正是最后一个与前一个模型相比 AICc 值有明显下降的模型。
## 带宽优选
带宽优选使用 `bw.gwr()` 函数,针对模型优选过程选出来的最优模型表达式 `model.formula` ,执行如下代码
```R
model.bw <- bw.gwr(formula = model.best.formula, data = londonhp, approach = "CV",
adaptive = T, kernel = "bisquare", longlat = F)
```
```plaintext
Adaptive bandwidth: 202 CV score: 508687382160
Adaptive bandwidth: 133 CV score: 493640667596
Adaptive bandwidth: 88 CV score: 486920162888
Adaptive bandwidth: 63 CV score: 490183342677
Adaptive bandwidth: 106 CV score: 4.90642e+11
Adaptive bandwidth: 79 CV score: 490124897035
Adaptive bandwidth: 95 CV score: 489323388109
Adaptive bandwidth: 84 CV score: 487487372346
Adaptive bandwidth: 90 CV score: 486546564806
Adaptive bandwidth: 92 CV score: 487660177626
Adaptive bandwidth: 89 CV score: 487330588439
Adaptive bandwidth: 90 CV score: 486546564806
```
返回值 `model.bw` 就是最优带宽。
## 模型拟合
函数 `gwr.basic()` 根据模型表达式 `formula` 和带宽 `bw` 对空间数据 `data` 拟合地理加权回归模型。
```R
model.gwr <- gwr.basic(formula = model.best.formula, data = londonhp, bw = model.bw,
adaptive = T, kernel = "bisquare", longlat = F)
```
```plaintext
***********************************************************************
* Package GWmodel *
***********************************************************************
Program starts at: 2022-03-20 16:39:02
Call:
gwr.basic(formula = model.best.formula, data = londonhp, bw = model.bw,
kernel = "bisquare", adaptive = T, longlat = F)
Dependent (y) variable: PURCHASE
Independent variables: FLOORSZ PROF UNEMPLOY
Number of data points: 316
***********************************************************************
* Results of Global Regression *
***********************************************************************
Call:
lm(formula = formula, data = data)
Residuals:
Min 1Q Median 3Q Max
-155570 -24625 -2373 19950 218206
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -159802.18 17042.15 -9.377 < 2e-16 ***
FLOORSZ 1469.29 65.76 22.342 < 2e-16 ***
PROF 352461.43 26396.36 13.353 < 2e-16 ***
UNEMPLOY 624800.97 124896.46 5.003 9.46e-07 ***
---Significance stars
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 43220 on 312 degrees of freedom
Multiple R-squared: 0.6746
Adjusted R-squared: 0.6715
F-statistic: 215.6 on 3 and 312 DF, p-value: < 2.2e-16
***Extra Diagnostic information
Residual sum of squares: 582680313106
Sigma(hat): 43077.49
AIC: 7648.68
AICc: 7648.874
BIC: 7380.238
***********************************************************************
* Results of Geographically Weighted Regression *
***********************************************************************
*********************Model calibration information*********************
Kernel function: bisquare
Adaptive bandwidth: 90 (number of nearest neighbours)
Regression points: the same locations as observations are used.
Distance metric: Euclidean distance metric is used.
****************Summary of GWR coefficient estimates:******************
Min. 1st Qu. Median 3rd Qu. Max.
Intercept -304980.9 -208164.1 -134318.3 -33059.1 97489.1
FLOORSZ 842.3 1086.1 1457.6 1894.2 2579.1
PROF -81821.1 122360.3 264760.0 372184.2 538140.1
UNEMPLOY -1097742.7 15001.4 553040.4 1194568.7 2171776.8
************************Diagnostic information*************************
Number of data points: 316
Effective number of parameters (2trace(S) - trace(S'S)): 38.58944
Effective degrees of freedom (n-2trace(S) + trace(S'S)): 277.4106
AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): 7534.642
AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): 7495.718
BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): 7322.187
Residual sum of squares: 337115746999
R-square value: 0.8117518
Adjusted R-square value: 0.7854706
***********************************************************************
Program stops at: 2022-03-20 16:39:03
```
通常,采用最优模型的表达式 `model.best.formula` 作为 `formula` 的值,最优带宽 `model.bw` 作为 `bw` 的值。返回值 `model.gwr` 就是你和的地理加权回归模型,在控制台中输出其结果即可得到模型的详细信息。
> ***虽然通常采用最优模型表达式和最优带宽,但并不意味着只能采用最优值。***
输出变量 `model.gwr` ,可以发现在 R 中展示了一系列模型分析的结果。结果分为三个部分,模型描述、全局回归结果、地理加权回归结果。通过这两个结果,可以对比地理加权回归模型的作用。
感谢您的阅读。本网站 MyZone 对本文保留所有权利。