论文快报:分层地理加权回归模型的后向拟合极大似然估计及其在北京市房价影响因子分析中的应用
2024年8月21日
科研
> **标题** > > A backfitting maximum likelihood estimator for hierarchical and geographically weighted regression modelling, with a case study of house prices in Beijing > > **作者** > > Yigong Hu, Richard Harris, Richard Timmerman, Binbin Lu > > **摘要** > > 地理加权回归(GWR)及其扩展是探索回归关系中空间异质性的重要局部建模技术。然而,当处理重叠样本的空间数据时——例如,为了避免泄露个别调查受访者的地址,将精确的位置信息汇总到共享的邻域——基于 GWR 的模型可能会遇到几个问题,包括获得可靠的带宽。由于具有这种特征的数据表现出空间层次结构,我们建议将分层线性建模(HLM)与 GWR 结合起来,提出一个分层和地理加权回归(HGWR)模型,该模型将系数分为样本级固定效应、组级固定效应、样本级随机效应和组级空间加权效应。本文提出了一种回归拟合似然估计器来拟合该模型,并通过模拟实验表明,HGWR 比传统的 HLM 或 GWR 模型更能捕捉这些效应及其内部的空间异质性,同时还通过一个案例研究探讨了中国北京房价的预测因素。 HGWR 同时处理空间和群体层次异质性的能力表明其作为处理具有空间层次结构的时空大数据的有前途的数据建模工具的潜力。 > > **DOI** > > [10.1080/13658816.2024.2391412](https://www.tandfonline.com/doi/full/10.1080/13658816.2024.2391412) # 什么是分层地理加权模型 简单来说,分层地理加权模型(Hierarchical and Geographically Weighted Regression, HGWR)模型是地理加权回归模型(GWR)和分层线性模型(HLM)的结合。该模型综合了 GWR 和 HLM 的优点,克服了 GWR 乃至多尺度 GWR(Multiscale GWR, MGWR)以及 HLM 在处理分层空间数据时的缺点。 ## 应用场景:分层空间数据 分层数据,通常指一组样本可以按照某种方式分为几类。常见的情况有学生按照所在学校分组、住房按照其类型分组、实验对象按照年龄分组等。在对数据进行建模时,同一个变量可能在不同组之间显现出不同的影响。如果不加以区分,可能会得出不显著的甚至是错误的结论。这种情况称为数据的组间异质性,即组与组之间是异质的。 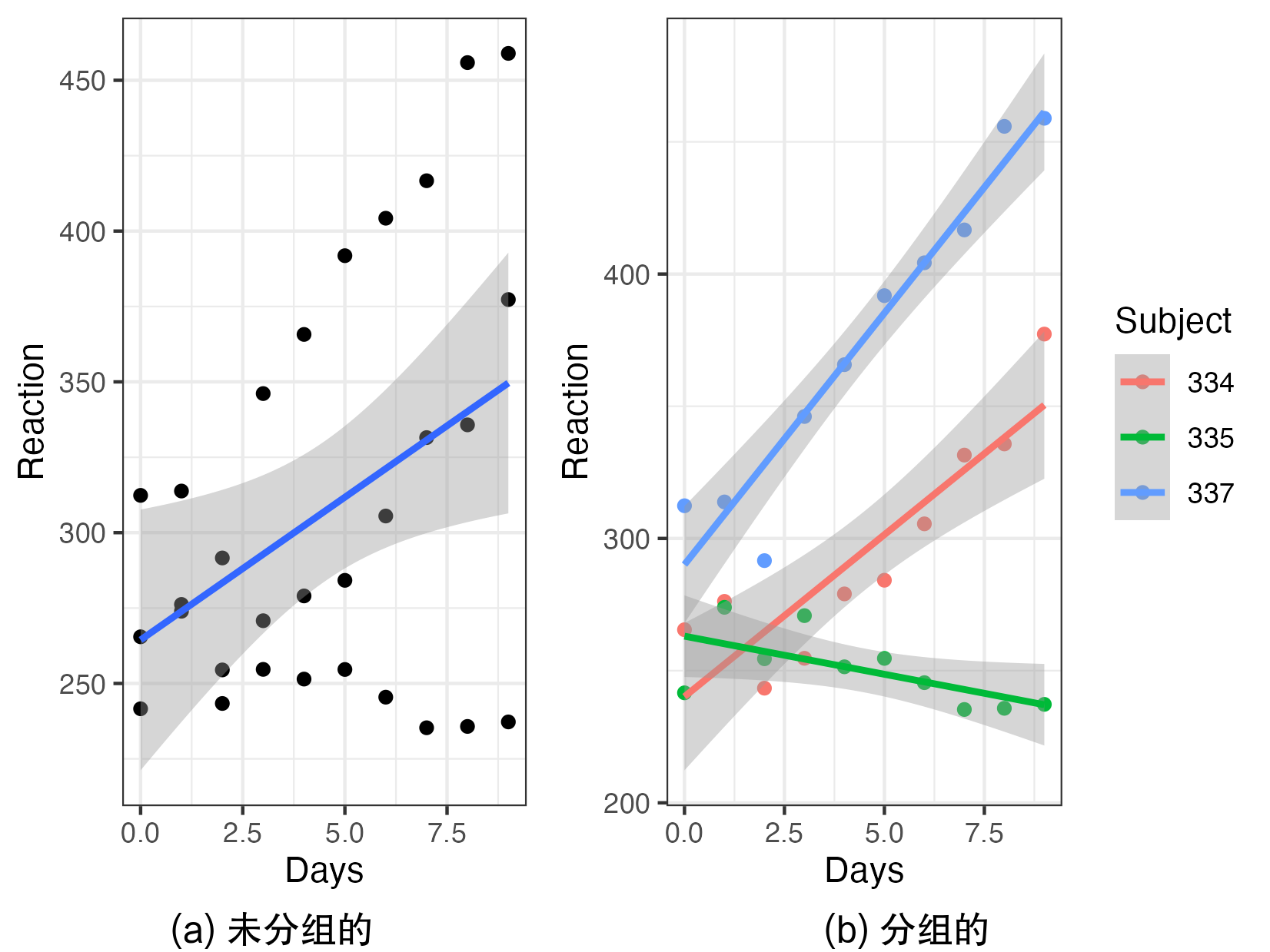 对于空间数据而言,由于空间位置的性质,很多空间数据天然就是分层的,例如调查数据可以根据其所在城市、省份划分为不同的组;房价数据可以根据所在小区、城市划分为不同的组;处方数据可以根据患者所在区域划分为不同的组。可以说,空间数据的位置信息是一个天然的分组标志。 然而,空间数据除了有「组间异质性」之外,还有「空间异质性」,也就是地理数据的某种性质随着空间的变化而变化。这种变化虽然会由于分组反映在组间异质性上,但也有其他未能反映的部分。这是因为考察分组异质性的前提是某个变量在组内取得不同的值,并据此估计该变量和因变量之间的线性关系。这种关系被称为「随机效应」。然而,一些变量在组内并不存在变化,例如高程、到水系的距离、人口密度等。这些变量的值与空间位置直接相关,当数据以位置为分组依据进行分组时,这些变量的值就不会发生变化,我们也就无从估计其对因变量的影响,而只能估计一个全局的影响。这种关系被称为「固定效应」。 这是目前的模型处理空间分层数据的主要问题:要么只考察组间异质性而不考虑空间异质性,要么只考虑空间异质性而不考虑组间异质性。 ## 模型改进:组间异质性与空间异质性 经过上述分析,我们可以看到现有模型的不足,具体地讲: - GWR 和 MGWR 模型没有考虑数据的分层特点,认为所有的样本都是独立的,对每个样本执行地理加权回归。这种处理没有考虑到组间异质性,而且对每个组内样本执行的是重复的解算过程。此外,当每组的样本数量不一致并且差异较大时,很有可能会造成在解算某个组时带宽过小,导致无法包含其他组的样本。此时如果包含了在每组中值不变的变量,就会产生奇异矩阵。 - HLM 考虑了组间异质性,并通过组间异质性反映空间异质性。然而,并不是所有空间异质性都可以通过组间异质性进行反映。HLM 模型无法处理这部分空间异质性。 HGWR 模型提出的目的就是要求解决这些问题。在 HLM 模型的基础上,保留随机效应的定义,将固定效应分成两类,一类仍然保留原本固定效应的估计方法,另一类则采用地理加权回归的估计方法,被称为「组级地理加权」(Group-level spatially weighted, GLSW)效应,或者也被称为「局部固定」效应。由于只有样本级变量在每组中有变化,导致只有样本级变量可以有随机效应,所以随机效应也被称为「样本级随机」(Sample-level random, SLR)效应。通过引入 GLSW 效应,解决 HLM 模型中无法考虑部分空间异质性而 GWR 模型中无法考虑组间异质性的问题。 # 如何求解 HGWR 模型 求解 HGWR 模型的过程主要用到的是后向拟合极大似然法(Backfitting and maximum likelihood, BFML),主要流程如下。求解过程涉及大量公式推导,感兴趣的读者可以点击阅读原文查看文章中的公式。  目前,我们也开发了一个名为 hgwrr 的 R 包,用于求解 HGWR 模型。该包支持普通的 DataFrame 或者 sf 格式的空间数据,并支持通过 R 语言的 formula 对象指定模型设置,还支持自动带宽优选。主要用法见下方的代码。更详细的介绍请移步[官方文档](https://hpdell.github.io/hgwrr/),有很多案例、API 介绍和与其他模型的对比结果。 ```R library(hgwrr) data(multisampling) hgwr( formula = y ~ L(g1 + g2) + x1 + (z1 | group), data = multisampling$data, coords = multisampling$coords, bw = "CV" ) ``` > 上述代码中,`L(g1 + g2)` 表示变量 `g1` 和 `g2` 拟合 GLSW 效应,`x1` 拟合固定效应,`z1` 拟合随机效应,按照变量 `group` 分组。带宽根据十字交叉验证方法进行优选。 # HGWR 模型效果如何 ## 模拟实验 我们生成了一组模拟数据,包含两个组级变量 $g_1$, $g_2$ 以及两个样本级变量 $x_1$, $z_1$,以及相应的 5 个回归系数 $\alpha_0$, $\gamma_1$, $\gamma_2$, $\beta_1$, $\mu_1$ (其中 $\alpha_0$ 是截距)。 利用该数据,拟合 GWR、MGWR、HLM 和 HGWR 四个模型,并对比系数估计值和真实值之间的差别。 | | GWR | MGWR | HLM | HGWR | | ------------------- | -------------------------- | -------------------------- | -------------------------- | -------------------------- | | Platform | Windows 11 | Ubuntu 22.04 | Windows 11 | Windows 11 | | Package (version) | GWmodel (2.2-9) | GWmodel (2.2-9) | lme4 (1.1-31) | hgwrr (0.3-0) | | CPU | Intel® Core® i7-11850H | Intel® Xeon® Gold 5118 | Intel® Core® i7-11850H | Intel® Core® i7-11850H | | Memory | 16GB | 256GB | 16GB | 16GB | | Threads | 15 | 48 | 1 | 1 | | Spent Time | 3.55 m | 4.41 h | 1.67 s | 6.06 s | > 模型解算时所使用的技术平台。  > 回归系数估计值和真实值的空间分布。 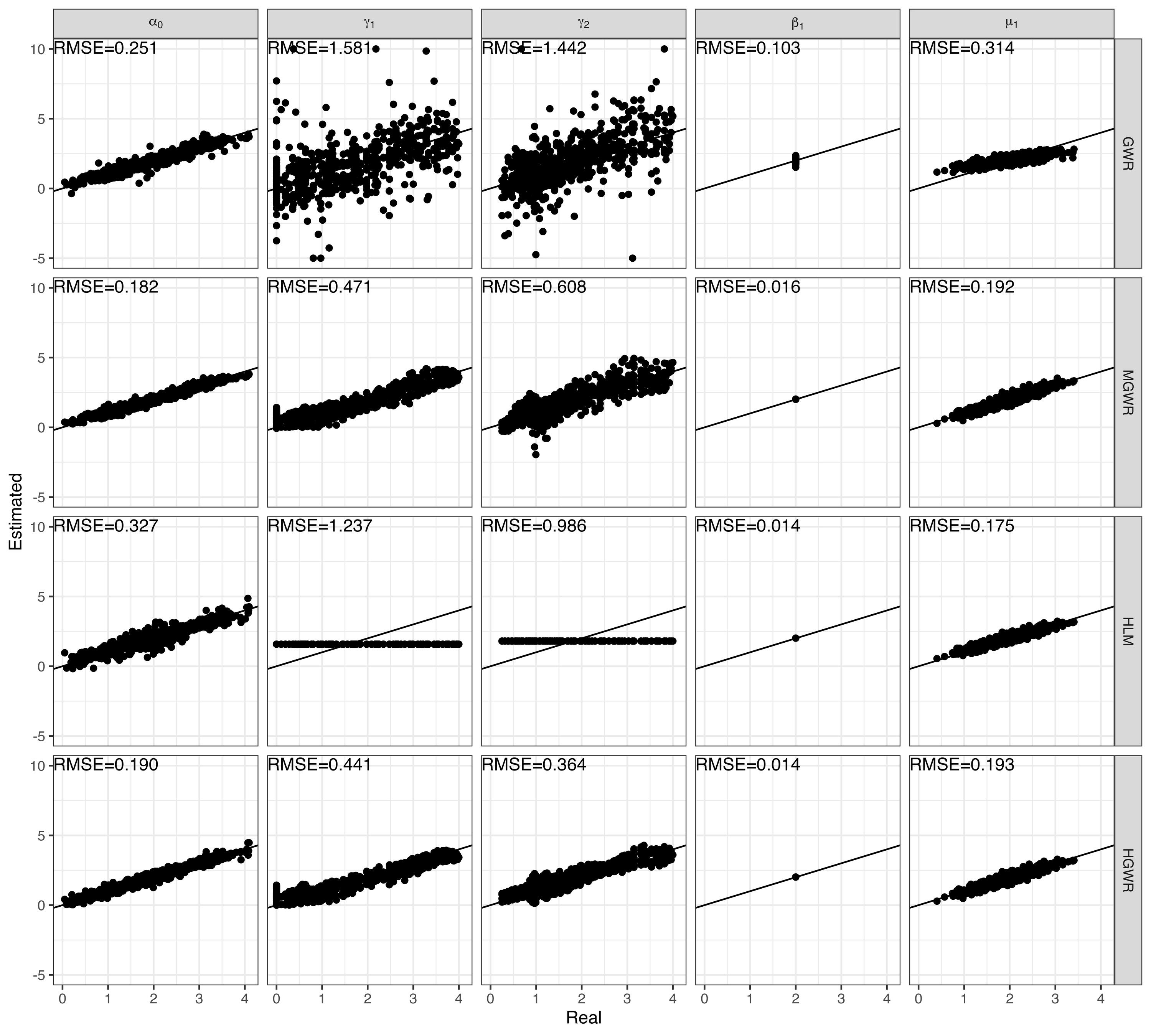 > 回归系数估计值与真实值线性关系。 从以上结果中我们发现,GWR、MGWR 和 HLM 都出现了一些问题。 1. GWR 对所有回归系数都进行了空间异质的估计,尽管有些变量(例如 $\beta_1$)并不具有空间异质性。而另一方面,$\mu_1$ 反而被平滑了。更重要的是,虽然带宽的大小有 234 个最近邻点,但只能覆盖 5-10 个位置,事实上覆盖的空间范围是比较小的。这就导致了 $\gamma_1$ 和 $\gamma_2$ 的估计过于局部,造成了图中所示的较大偏差。 2. MGWR 虽然部分克服了 GWR 中的问题,但仍然有一些问题没有解决。对于 $\beta_1$ 而言,MGWR 依然给出的是具有空间异质性的估计,虽然这种空间变化很微弱,在图中不明显。另一方面,由于地理加权过程的存在,$\mu_1$ 的估计依然体现出某种被平滑的特点。然而这种地理加权的过程是不必要的,因为在每个位置上已经有足够多的样本进行系数估计。除此之外,求解 MGWR 模型的计算量非常大,当样本数量较大时,对内存的需求也很大。 3. HLM 模型解决了 GWR 和 MGWR 中的问题,即 $\beta_1$ 和 $\mu_1$ 的估计比较符合预期。然而,问题出在对 $\gamma_1$ 和 $\gamma_2$ 的估计上。由于 $g_1$ 和 $g_2$ 是组级变量,我们无法估计随机效应,只能估计固定效应。这导致 $\gamma_1$ 和 $\gamma_2$ 的估计是全局一致的,而我们希望得到具有空间异质性的估计。 最终,我们发现 HGWR 同时解决了上述所说的问题。该模型既可以对 $\gamma_1$ 和 $\gamma_2$ 进行具有空间异质性的估计,也可以对 $\beta_1$ 进行全局一致的估计,还避免了对 $\mu_1$ 估计的平滑效应。尽管 HGWR 获得的估计值仅比 MGWR 略有改进,但它消耗的计算时间要少得多,大约只有几秒钟,且对内存的需求也很小。 上述实验经过 100 次重复,每次重复时随机生成一批变量,但保持回归系数不变(由于 MGWR 太过耗时,这里就舍弃了)。通过统计回归系数估计值的均方根误差,我们发现 HGWR 模型不仅降低了误差均值,还降低了误差的方差。 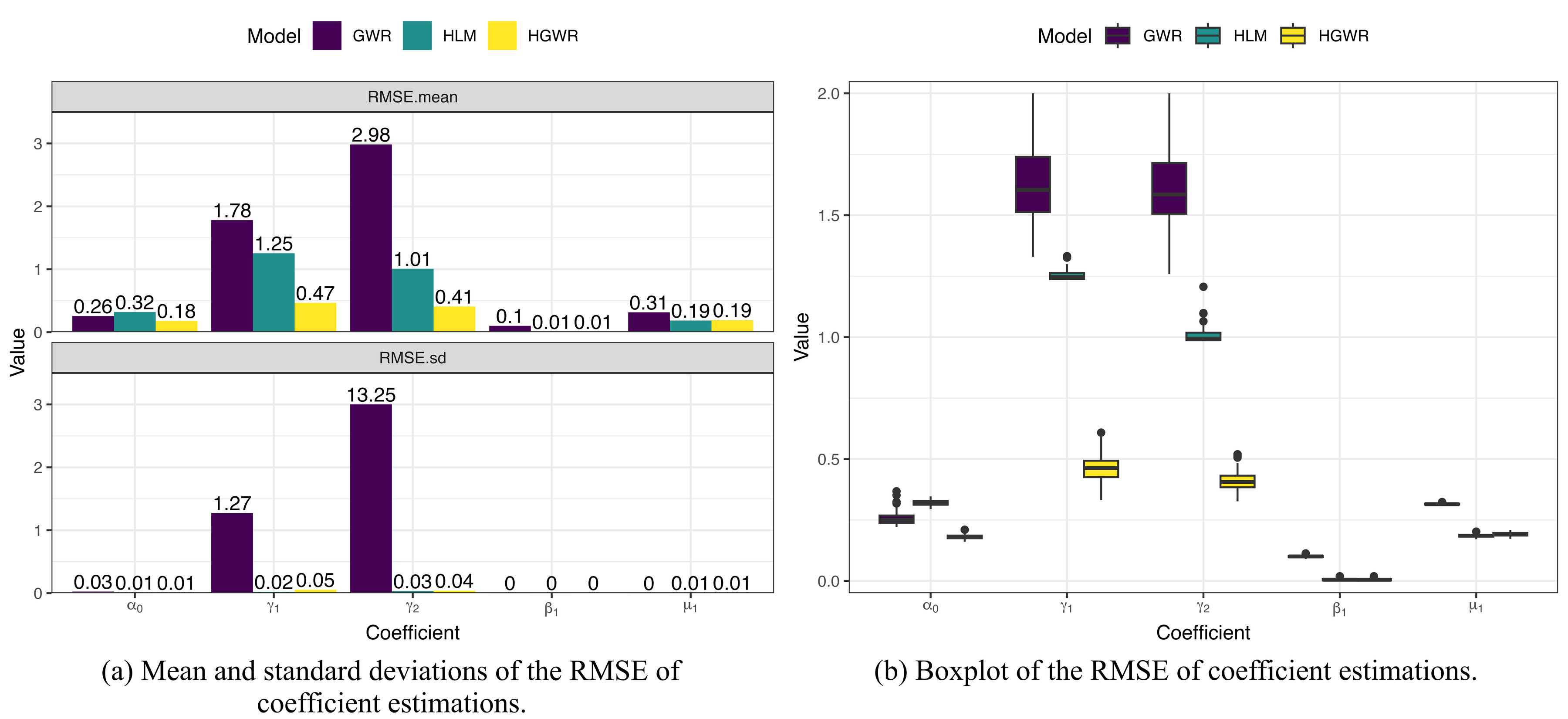 > 回归系数均方根误差的分布。 ## 案例研究 为了研究 HGWR 模型在真实案例中的表现,我们获取了北京市二手房房价数据和 POI 数据。需要注意的是,该案例研究的目的是为了证实 HGWR 模型在真实数据中可用,而不是准确地找到北京市房价的影响因素。为了保持模型简洁以方便对比,我们只选取了少量的变量,分析模型在这些变量上得到的回归系数的特点,从而验证模型的可行性。  > 北京市中心几个区的二手房房价数据。每个点代表了一个二手房,颜色代表了房价。同一个小区内的二手房共享一套坐标。 由于带宽是 GWR 和 HGWR 中的关键参数,它们通过交叉验证分别优化为 561 和 45 个最近邻。请注意,GWR 模型中的“邻居”指的是属性,而 HGWR 模型中的“邻居”指的是包含这些属性的公寓小区。当将 GWR 选择的自适应带宽值转换为每组的最近小区数量时,我们发现它们从 8 到 35 不等,这意味着 561 个最近属性的带宽值实际上覆盖了 8 到 35 个小区,其中大多数覆盖了 25 个小区。因此,带宽比 HGWR 模型选择的要小。MGWR 也出现了类似的情况,有些带宽甚至更小:许多变量的带宽,如地铁、咖啡馆和火车站,范围从 2 到 16 个小区。尽管我们不知道这些变量的实际规模,但如此小的带宽确实增加了过拟合的风险。此外,不同带宽(在公寓小区尺度上)导致不同位置的估计空间尺度不同——这种变化并不符合实际的空间尺度,而是受样本大小的影响。 下表展示了几个模型的 $R^2$ 值。虽然 MGWR、HLM、HGWR 的 $R^2$ 比较接近,但是细究下来会发现有很大的区别。HLM 能够达到如此之高的 $R^2$ 值的原因在于拟合了随机截距。随机截距将捕获组级变量的空间异质性。相反,HGWR 将这种空间异质性归因于 GLSW 效应,以提供更好的可解释性。对于 MGWR 而言,非常局部的带宽对 $R^2$ 值有很大贡献。然而,这一过程需要几天时间以及通常难以支付的内存需求(大约 83 GB)。相反,HGWR 模型只需要很少的时间和内存空间却可以达到更好的拟合效果。可以预见的是,随着数据量的增加,MGWR 所需算力将会急剧增长。然而,只要组的数量固定,HGWR 模型的时间复杂度不会有太显著的提升。 | Model | (Pseudo) R2 | Adjusted R2 | Marginal R2 | Conditional R2 | | :-----: | :-----------: | :-----------: | :------------: | :---------------: | | GWR | 0.810 | 0.799 | | | | MGWR | 0.847 | 0.835 | | | | HLM | 0.870 | | 0.117 | 0.852 | | HGWR | 0.876 | | | | 下面这些图展示了(部分)回归系数的分布模式。 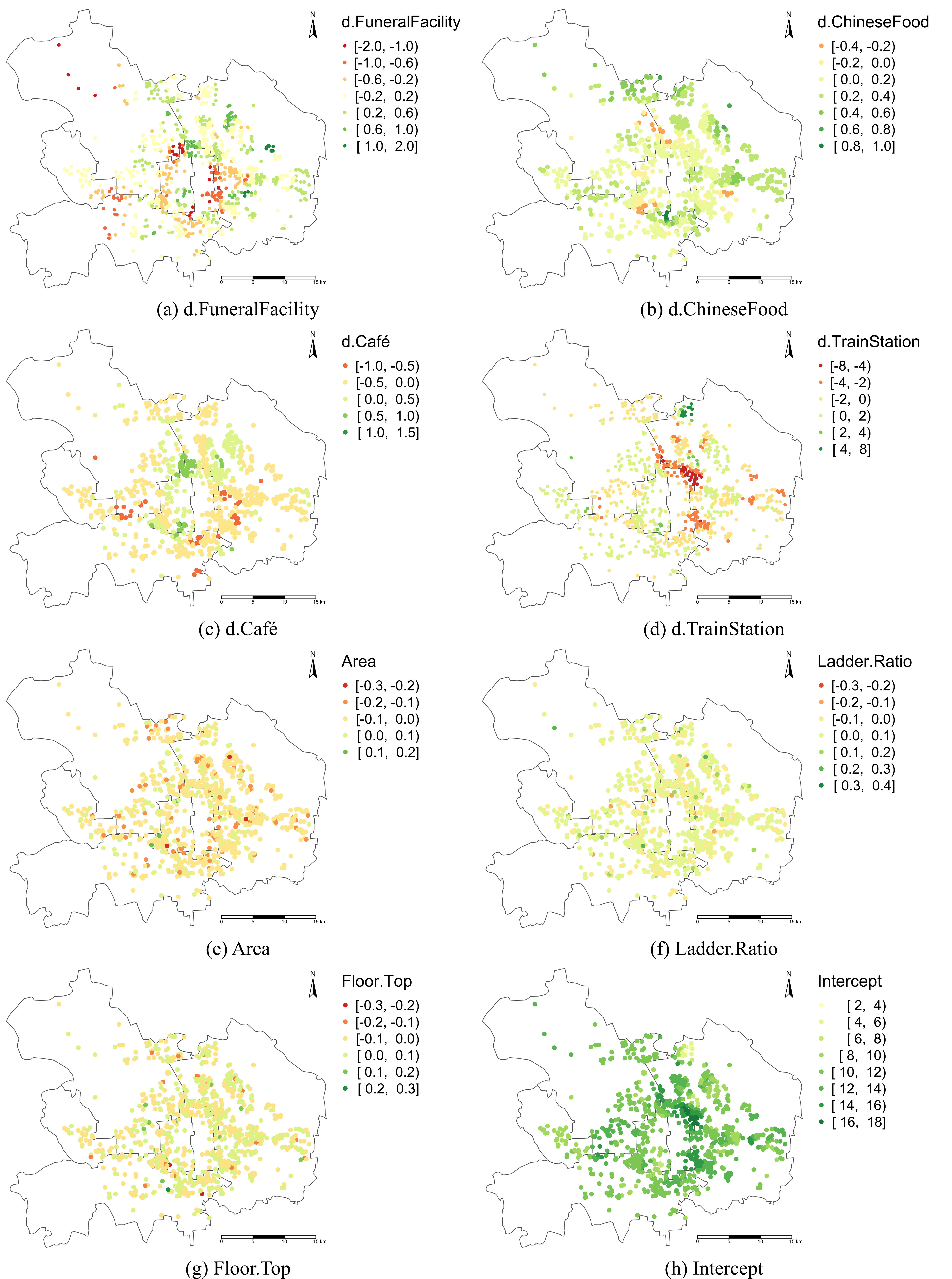 > HGWR 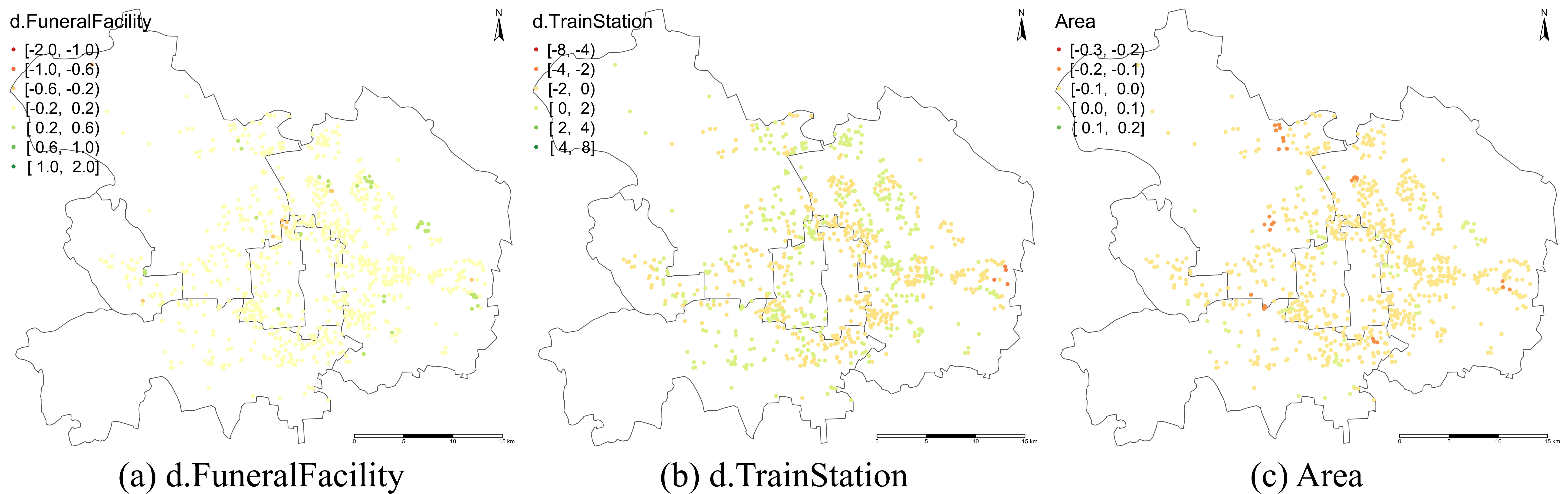 > GWR 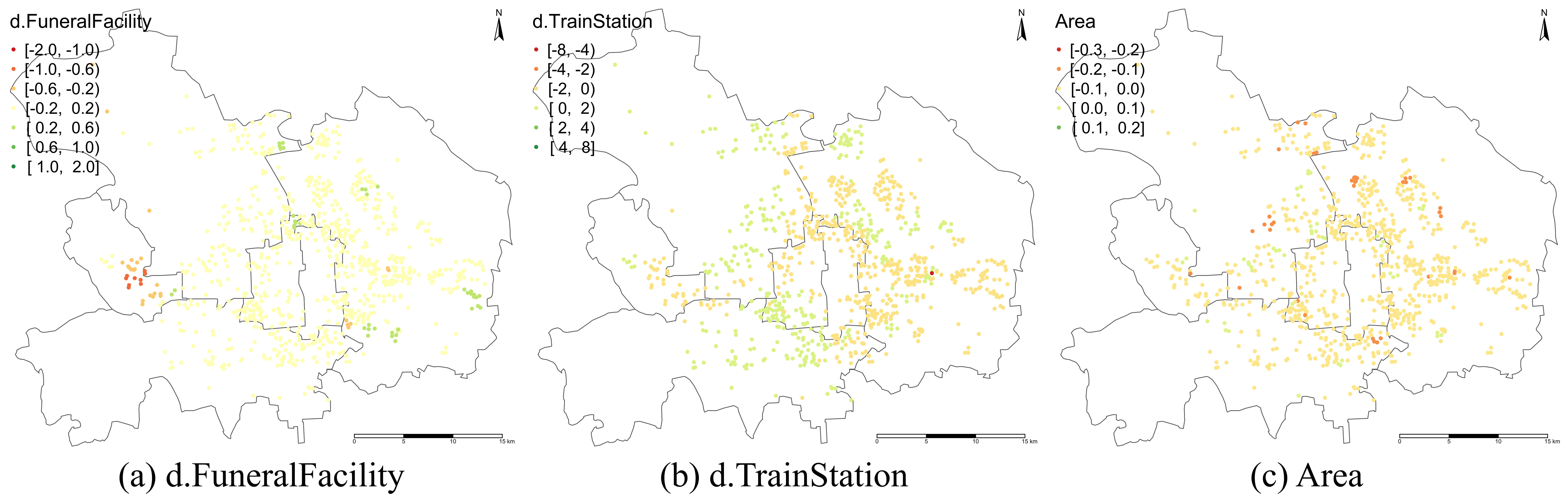 > MGWR 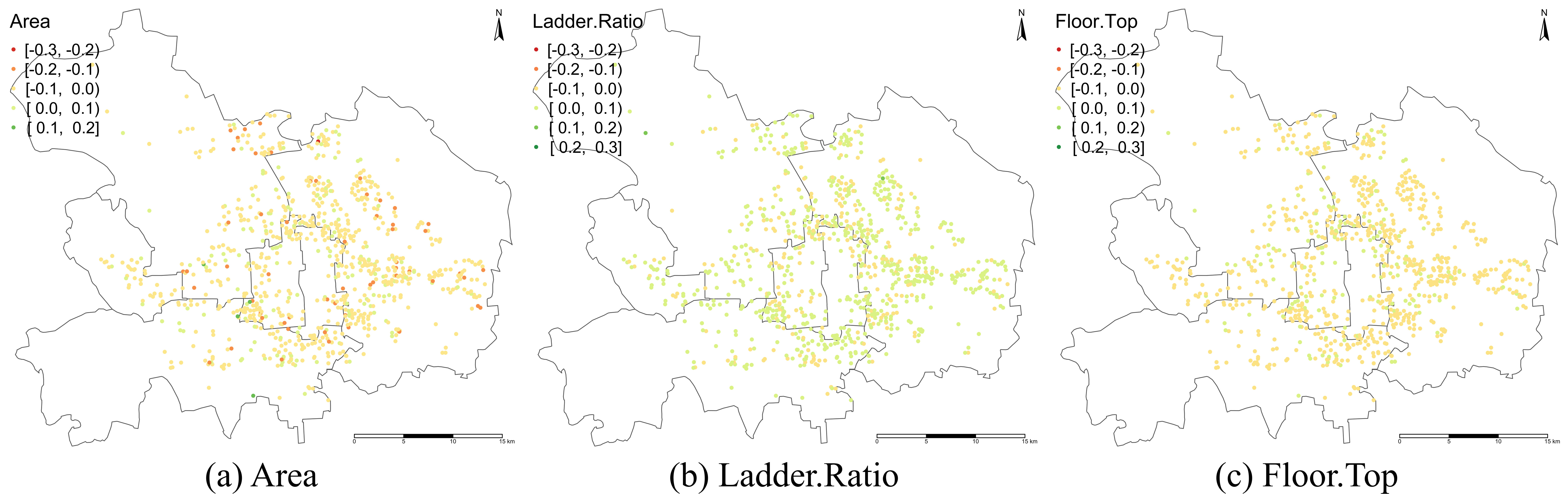 > HLM 我们依然可以发现与模拟实验中类似的现象。与 GWR 和 MGWR 模型的系数估计相比,HGWR 模型中 d.FuneralFacility 和 d.TrainStation 效应估计的空间趋势是恒定的,不受每组样本数量的影响。然而,GWR 和 MGWR 在某些位置给出的估计是高度局部的,因为这些位置包含更多的样本。事实上,不仅仅是图中所显示的效应,其他效应也有潜在过拟合的问题。HLM 和 HGWR 模型在随机效应上得出了相似的结论,却在组级变量上无法进行具有空间异质性的估计。由于随机效应系数值的实际值未知,我们并不判断 HGWR 比 HLM 更正确,反之亦然。相反,我们认识到它们给出了相似的结果,并预计两者在估计 SLR 效应方面都是可靠的。然而,HGWR 具有计算优势。 # 进一步的讨论 抛开数据与实验,我们想讨论三个问题: 1. HGWR 与 MGWR 有何不同? 2. 为什么 GLSW 效应在多层次建模中很重要? 3. 以及如果数据不完全重叠(即样本的位置在组内不完全重合)会发生什么? 尺度是地理分析中一个非常重要的概念。MGWR 相比其他 GWR 模型能够具有更好的拟合优度的原因在于它同时考虑了多个空间尺度(按变量)。从空间尺度的角度来看,HGWR 和 MGWR 都是“多尺度”模型,但它们以不同的方式应用不均匀的尺度。MGWR 假设每个样本处于一个独特的位置,而 HGWR 假设数据在几个位置内重复。对于不同类型的变量,HGWR 在三个尺度水平上估计它们的效应:全球尺度、局部尺度和组内尺度。MGWR 不考虑组内尺度;然而,HGWR 目前不允许局部尺度对不同变量变化,因为只有一个带宽,而 MGWR 在估计系数时应用特定参数的局部尺度(带宽)。尽管这意味着更高的计算成本,但将 HGWR 扩展到多尺度版本是可能的。 理论上,如果在一个位置提供足够的样本 $u_i$,就有可能在不借用(核加权)邻居样本的情况下拟合线性回归模型。这就是为什么 SLR 效应可以揭示样本级变量的空间异质性。然而,这种做法要求矩阵 $X$ 是完全秩的。一旦有些变量的值(主要)由位置决定(例如 $x=f(u_i)$,其中 $f$ 是一个函数),它们可能导致 $X$ 不满秩。遗憾的是,这通常是群体级地理变量的情况。我们可以为它们分配固定效应(如 HLM)或 GLSW 效应。当存在空间异质性时,后者是更好的选择。最终,HGWR 解决了估计空间异质性和群体级变量固定效应之间的冲突。 在一些新的行政和其他数据来源中,出于数据隐私的原因,个人(或家庭等)的确切地理位置不会被公开,只有更为聚合的分组和地理标识符(例如人口普查边界)是已知的。这种数据审查创建了一个属于群体级地理的两级结构。对于其他数据,样本的坐标不一定是“未知”的,也不一定完全重叠,尽管本文假设如此。当样本位置接近,表明它们之间没有显著的空间变化时,它们仍然可以被视为一个群体。在任何情况下,使用 GWR 系列模型(包括 MGWR)可能会违反样本之间存在空间异质性的假设。如果使用 HLM,群体级变量中的不显著异质性仍不足以拟合随机效应。最后,我们提出 HGWR 作为建模这种数据的潜在解决方案。只要每个群体内没有显著的空间异质性,样本是否完全重叠并不重要。 然而,仍有一些限制需要解决。例如,由于 BFML 是迭代的,因此有必要更好地理解最佳初始值以及在什么条件下它们会收敛。除此之外,尽管回归框架很直接,但在某些情况下它可能过于灵活。我们认为贝叶斯框架或马尔可夫链蒙特卡罗估计器可能提供潜在的替代方案。它们不仅在估计中表现出更大的稳定性(Dong 和 Harris 2015),而且允许结合先验知识,从而有助于更好地处理当前算法无法实现的空间依赖性。最后,显著性检验方法是不可或缺的,因为它们有助于识别重要变量并开发变量规范方法。尽管通过 HGWR 可以准确估计参数,但这并不一定意味着它们在统计意义上是显著的。我们正在探索基于自助法或置换检验的 HGWR 参数检验方法。 总之,HGWR 是为一种特殊但并不罕见的数据设计的,这种数据包括每个位置的多个样本,以及一些由位置决定的组级变量。对于第一个条件,HGWR 比 GWR 系列方法更灵活,因为它可以处理层次结构。对于后一个条件,HGWR 比 HLM 更好,因为它使组效应可以在不同位置之间变化。当这两个条件中的任何一个消失时,HGWR 会简化为现有模型。然而,随着时空大数据的普及,HGWR 所设计的特定参数和数据结构的情况变得越来越普遍,这表明 HGWR 作为分析此类数据的有价值工具具有相当大的前景。
感谢您的阅读。本网站 MyZone 对本文保留所有权利。