原神中为什么暴击暴伤比为1:2最好？

原神中的圣遗物属性搭配是一个既烧摩拉又有趣的问题。相信很多玩家听说过一个结论，“角色面板暴击暴伤比为1:2时，期望伤害最高”。那为什么会得到这个结论呢？这涉及到很多有趣的数学问题，这篇博客中我们尝试进行推导。但是，由于实际角色伤害还取决于攻击力，但是引入攻击力的会使问题变得很复杂，这里就认为攻击力是不变的。确切地说，是在更换不同圣遗物或武器后，角色攻击力保持不变。

视频版：

<div class="ratio" style="--bs-aspect-ratio: 62.5%;">
<iframe src="https://player.bilibili.com/player.html?aid=425781836&bvid=BV1s3411T7Qt&cid=579186892&page=1" scrolling="no" border="0" frameborder="no" framespacing="0" allowfullscreen="true" width="100%"> </iframe>
</div>

# 伤害的数学期望

暴击率、暴击伤害，是动作游戏中很经典的两个属性。暴击率，就是指角色在一次攻击时发生暴击的概率。在原神中，假设一名角色的暴击率是 $p$，暴击伤害是 $q$，在不暴击的时候，伤害总值是 $a$，那么在攻击发生暴击时，当次攻击的伤害变为 $(1+q)a$。那么，对于攻击造成伤害这一事件，其取值 $A$ 服从如下分布列：


| $A$ |  $a$  | $(1+q)a$ |
| :---: | :-----: | :--------: |
| $P$ | $1-p$ |   $p$   |

那么一次伤害的数学期望值 $e$ 就有

$$
\begin{aligned}
e = E(A)
&= (1-p)a+p(1+q)a \\
&= a + pqa \\
&= (1+pq)a
\end{aligned}

$$

在我们当前的假设中，可以认为 $a$ 是一个常数，$p$ 和 $q$ 是两个变量。那么我们分解将 $e$ 对 $p,q$ 求偏导，

$$
\frac{\partial e}{\partial p} = qa, \quad \frac{\partial e}{\partial q} = pa

$$

由于 $a,p,q$ 都是正数，所以理论上，**暴击率越高，暴击伤害越高，伤害期望也越高**。但是这似乎与之前的结论矛盾。为什么会出现这个情况呢？

# 伤害期望的约束最大值

事实上，这是由于原神中“圣遗物”系统和“武器”系统的特性决定的。上述结论没有考虑到暴击率和暴击伤害取值的约束条件。下面先简述一下圣遗物和武器系统，来找到问题中的约束条件。

## 圣遗物和武器系统简介

原神中每个人物最初始的情况下，有 5% 的暴击率和 50% 的暴击伤害。出了每个人物突破会提升暴击率暴击伤害以外，这个数值可以通过装备不同的圣遗物和武器进行提升。原神中每个人物最多装备5件圣遗物和1把武器，每件圣遗物（按五星计算）有1个主属性和4个副属性，每把武器有一个主属性和一个副属性。对于圣遗物而言，有以下几条约束：

- 圣遗物中只有“理之冠”（俗称“头”）有可能是暴击率或暴击伤害；每件圣遗物的副属性都有可能是暴击率和暴击伤害。但是所有主属性和副属性都不可能有重复的属性。
- 每件圣遗物最多强化到20级，每次升级都会强化主属性，但每提升4级才会提升一次副属性（如果副属性不足4个则有限生成一个副属性）。
- 每次强化虽然会强化到不同的属性，但是数值的比例是大概相同的，以使属性“总量”不会发生太大的变化。也就是说，不会出现一次强化出现100%暴击率的情况。
- 每次提升属性时，提升到暴击率和暴击伤害的数值大约是 $1:2$ 的比例，也就是说，在一次提升时，如果提升的是暴击率且提升了3.8%，那么如果这次提升发生在暴击伤害上，则提升量大约是7.6%。

对于武器而言，相对来说就简单很多。每把武器的主属性必然是攻击力，副属性虽然可能是暴击率或暴击伤害，但都是确定的。级如果只看副属性是暴击率或暴击伤害的武器（俗称“暴击武器”或“暴伤武器”），平均每次升级时暴击率和暴击伤害提高的数值差不多也是 $1:2$ 的比例。

在这样的情况下，我们可以假设一个暴击率和暴击伤害的总量 $c$ ，这个量和暴击率与暴击伤害的关系就是

$$
c=2p+q

$$

这将成为我们计算期望伤害最大值的约束条件。但事实上，我们不可能保证两件圣遗物的暴击暴伤总量完全相同，这里只是做一个理论计算，分析暴击率和暴击伤害的最佳配比。

## 暴击暴伤总量不变情况下的伤害期望最大值

根据之前推导的伤害期望 $e$ 与暴击暴伤的函数关系，设角色和武器自带的暴击率为$p_0$，自带的暴击伤害为$q_0$，圣遗物提供的暴击暴伤分别是$p,q$，结合暴击暴伤总量 $c$ 与暴击爆伤函数关系的约束条件，有

$$
\begin{aligned}
e &= [1+(p+p_0)(q+q_0)]a \\
c &= 2p + q
\end{aligned}

$$

要求 $e$ 的约束最大值，可以使用[拉格朗日乘数法](https://baike.baidu.com/item/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0%E6%B3%95/8550443)，构造 $\phi=2p+q-c$ ，$F=e+\lambda\phi$，可以得到下面的方程组

$$
\begin{aligned}
\frac{\partial F}{\partial p} & = (q+q_0)a+2\lambda = 0 \\
\frac{\partial F}{\partial q} & = (p+p_0)a+\lambda = 0 \\
\frac{\partial F}{\partial \lambda} &= 2p+q -c = 0
\end{aligned}

$$

通过解上述方程组可以很容易得到，当 $q=2p=\frac{1}{2}(c+2p_0-q_0)$ 的时候，函数 $e$ 取得极值，此时 $\lambda=-\frac{1}{4}(c+2p_0+q_0)a$。由于此时$c,p_0,q_0$都是常数，为了方便起见，我们可以有$c'=c+2p_0-q_0$，并重新将这个值记为$c$。而由于极值点只有这么一个，所以这个就是最值点。那么这个是最大值还是最小值呢？

一种方法是，由于一般 $p \in [0.05,1]$ 而 $q\in[0.5, q_m]$，这里的 $q_m$ 是所有装备暴伤拉满时的数值。这个数值虽然我没有见过，但是肯定是存在而且确定的。虽然不知道，但没关系，因为当 $p=0.05$ 时，$q=c-0.1$，此时 $pq=0.05c-0.005$；而当 $p=\frac{1}{4}c$ 时，$pq=\frac{1}{8}c^2$。令

$$
g=\frac{1}{8}c^2-\frac{1}{20}c+\frac{1}{200} = \frac{1}{8}\left(c-\frac{1}{5}\right)^2

$$

显然，$g \geqslant 0$ 恒成立，当且仅当 $c=0.2$ 时 $g=0$。而人物的原始面板就已经保证了 $c=0.6$ ，搭配装备后只会使得 $c\geqslant 0.6$，所以 $\frac{1}{8}c^2 \geqslant 0.05c-0.005$ 。所以，当 $q=2p=\frac{1}{2}c$ 的时候，函数 $e$ 取得极大值。

另一种方法是，画个图看一下。用 Geogebra 画出这几个（隐）函数的图像，再把这个极值点标出来，就知道时最大值还是最小值了。

![image.png](/media/81a24d88-f58d-4e91-ad1c-2ca90e54b0ca_image.png)

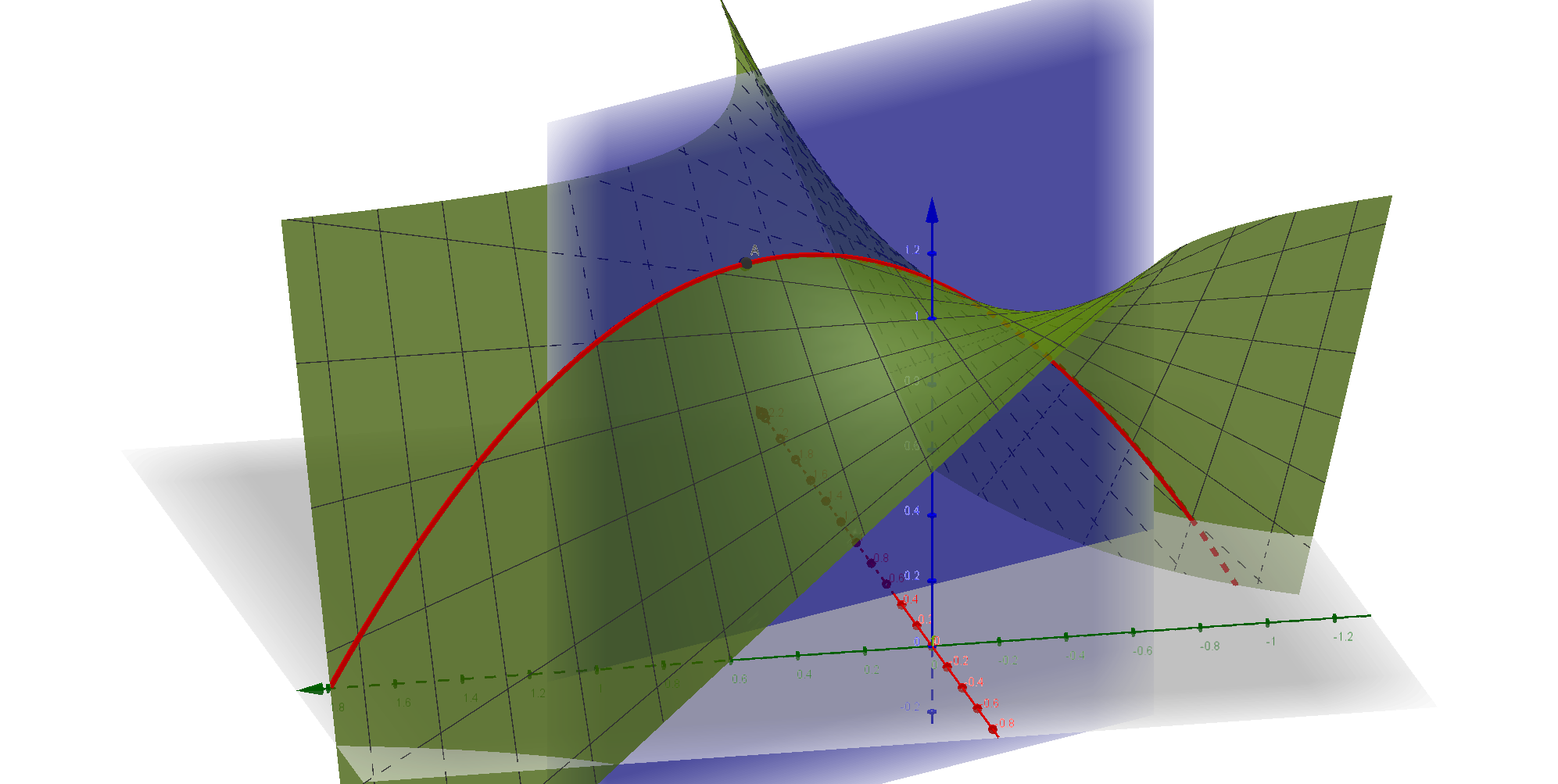
图中蓝色的绿色的曲面代表了函数 $e$ ，蓝色的平面代表了约束条件，红色的曲线就是满足约束条件时 $e$ 的可能取值，黑色的点就是极值点。显然，这是一个最大值点。

由此，我们最终得到结论：**在暴击暴伤总量 $c$ 不变的情况下，当暴击率与暴击伤害比值为 $1:2$ 的时候，伤害期望是最高的**。

# 暴击头还是爆伤头

当角色有暴击武器或者暴伤武器的时候，这不是问题。由于属性稀释，直接选择另一个属性的理之冠即可。但是当角色没有暴伤武器或者暴击武器的时候，例如迪卢克和狼的末路，那么理之冠是选择暴击头还是爆伤头呢？

我们先假设其他圣遗物副属性完全没有暴击暴伤的情况，有暴击暴伤的情况请参考后文。

当选择暴击头时，$p=0.361$ ，$q=0.5$ ，$pq=0.1802$ 。

当选择暴伤头时，$p=0.05$ ，$q=1.122$ ， $pq=0.0561$ 。

这样就一目了然了，优先选择暴击头。那么这是什么原因呢？

一种简单的理解是属性稀释。确实，暴伤也是会被稀释的。其实几乎所有属性都会被稀释，而当属性提升前的值 $x_0$ 越高时，提升量 $x$ 的稀释越严重。因为提升度 $t$ 有

$$
t = \frac{x}{x_0+x}, \frac{\partial t}{\partial x_0} = -\frac{x}{(x_0-x)^2}

$$

所以 $t$ 随 $x_0$ 的增大而减小。暴伤基础值是 0.5，暴击基础值是 0.05 ，所以装备暴击头时提升幅度有8倍，但是带暴伤头时提升幅度只有2倍，所以最好带暴击头。

另一种理解，我们其实可以算出来消灭一只怪物所需要的平均攻击次数（这里简化一下）。因为怪物的血量 $m$ 是一定的，所需要的攻击次数 $n$ 就应该有

$$
\begin{aligned}
n&=\frac{m}{e}=\frac{m}{(1+p(c-2p))a} \\
\frac{\partial n}{\partial p}&=-\frac{m}{e^2}(c-4p)a
\end{aligned}

$$

当 $p<\frac{1}{4}c$ 时，$n$ 递减，当 $p<\frac{1}{4}c$ 时，$n$ 递增。而只有理之冠的主属性有暴击暴伤时， $c$ 基本上是 1.222，所以其实 $p=0.3055$ 时，需要的攻击次数是最低的。而且，由于 $n$ 在大于0的部分是对称的，对称轴是 $\frac{1}{4}c$ ，所以装暴击头时 $p$ 的值离对称轴更近，所以总攻击次数更小。

对于[迪卢克](https://bbs.mihoyo.com/ys/obc/content/75/detail?bbs_presentation_style=no_header)这种突破加暴击的角色，满级时暴击率是 0.242，暴击暴伤总量 $c$ 达到 1.606 。装备暴击头时，$p=0.553$ ，与 $c/4$ 差距是 0.1515；装备暴伤头时，暴击率与 $c/4$ 差距是 0.1595。所以还是装备暴击头更好，当然差距不大，完全可以看副属性那个好带那个。

此外还有一点，迪卢克是一个爆发不是很离谱的角色。对于[优菈](https://bbs.mihoyo.com/ys/obc/content/2040/detail?bbs_presentation_style=no_header)这种爆发离谱的角色，暴击率带高一些可以少凹几次，减少痛苦。

当然对于[胡桃](https://bbs.mihoyo.com/ys/obc/content/1627/detail?bbs_presentation_style=no_header)这样，突破加暴伤，暴伤专武，就不用纠结了，最终还是配平暴击暴伤比，并且暴击暴伤越高越好。

# 更深入的分析

有一些问题在前面的文章中确实没有解决：如果暴击暴伤比为1:2最好，那暴伤是不是最多堆200%？但是显然，如果圣遗物足够极品，暴伤能堆超过200。除了这个问题，还有一些问题也不是现在这个1:2理论可以解释的。比如说，为什么大家都说暴击率一般堆到70%然后堆爆伤。再比如，为什么有的角色带暴击头更好，有的带暴伤头更好。

为了解决这些问题，我们对暴击暴伤的来源做进一步的细化。由于头部位置主属性可能是暴击或暴伤，而副属性永远不会和主属性重复，这也就意味着暴击暴伤总量 $c$ 的计算没有那么简单。我们假设角色+武器的基础暴击率为 $p_0$ ，基础暴击伤害为 $q_0$ ，理之冠的暴击率为 $p_1$ ，暴击伤害为 $q_1$ ，其他圣遗物的暴击率和暴击伤害分别为 $p,q$。注意，如果我们假设理之冠满级且副属性的暴击/暴伤拉满，那么此时 $p_1,q_1就不再是变量了，而是固定值。那么伤害期望及约束条件是

$$
\begin{aligned}
e &= \left[ 1+(p+p_0+p_1)(q+q_0+q_1) \right]a \\ 
c &= 2p + q
\end{aligned}

$$

用原文中同样的求解方法，可以得到

$$
\begin{aligned}
p &= \frac{1}{4}(c - 2p_0 - 2p_1 + q_0 + q_1) \\ 
q &= \frac{1}{2}(c + 2p_0 + 2p_1 - q_0 - q_1)
\end{aligned}

$$

如果我们带入护摩胡桃的数据，基础暴击率5%，基础暴击伤害154.6%，所有圣遗物都强化在暴击暴伤上，即 $c=2.176$ ，根据理之冠的情况：

- 如果装备暴击头，那么极值点 $(p,q)=(0.8665,0.4430)$ ，总暴击总暴击122.75%，暴伤245.50%。
- 如果装备暴击头，那么极值点 $(p,q)=(0.9445,0.2870)$ ，总暴击总暴击122.75%，暴伤245.50%。

但如果装备暴伤头，$p$ 法达到极值点，因为其最大值是93.2%。如果我们把溢出的暴击率分配到暴击伤害上，那么可以发现此时期望伤害值是相等的。也就是说如果圣遗物足够极品，胡桃带上护摩头也不是不行，就是难度实在是太高了。考虑到副词条升级的难度，还是带上暴击头，这样能尽快提高暴击率，其他圣遗物也更容易毕业。

同时我们也会发现，装备暴击头的护摩胡桃，如果圣遗物全是极品，暴伤就已经达到了245.5%，已经超过了200%。所以即便遵循暴击暴伤比1:2，暴伤也是应该超过200%的。但是这显然不会是我们所希望的配装，因为暴击已经溢出了22.75%！所以，如果我们把溢出的暴击按比例加到暴伤上，那么暴伤将会达到291%。这已经不是往生堂堂主了，这是往生堂战神。当然，虽然没有经过计算，但我觉得这种情况出现的概率，应该不会高于十连满命的概率。所以如果我们实际的圣遗物在数值上比这个理想值低，那么暴伤依然有可能超过200%。

那既然暴击率的极值点往往超过了100%，又为什么一般要求圣遗物暴击率堆到70%呢？我觉得还是概率大小的问题，而且对于不同角色这个值也不是一成不变的。对于一件初始具有双暴属性且所有强化都强化在双暴属性上的圣遗物，最终双暴值的分布情况，一共有83种可能的暴击率的值。对于护摩胡桃这种突破和专武都不加暴击率的角色，在装备暴击头的情况下，其他四件圣遗物暴击率至少要8.475%的暴击率，而强化出这样一件圣遗物的概率是79.3%，属于是“初始具有双暴属性且所有强化都强化在双暴属性上”情况下的大概率事件。但是考虑到圣遗物的实际出货情况，不一定四件全都有双暴；即使你有一套全双暴的圣遗物，也很难全都强化到双暴属性上。如果对暴击率要求再高，那基本上就永远不能毕业了。再考虑到原神作为PVE的RPG游戏，没有必要追求满暴，大不了多打几下。

除了胡桃以外，其他角色也适用上述分析方法。下面我列出了一些不同特点的角色和武器组合情况下的暴击暴伤情况。


| 角色突破 | 角色举例 | 武器副属性 | 武器举例     | 基础暴击 | 基础暴伤 |
| ---------- | ---------- | ------------ | -------------- | ---------- | ---------- |
| 暴伤     | 胡桃     | 暴伤       | 护摩之杖     | 5%       | 154.6%   |
| 暴伤     | 神里绫人 | 暴击       | 波乱月白经津 | 38.1%    | 88.4%    |
| 暴击     | 宵宫     | 暴伤       | 飞雷之弦振   | 29.2%    | 116.2%   |
| 暴击     | 魈       | 暴击       | 和璞鸢       | 46.3%    | 50%      |
| 暴伤     | 优菈     | 其他       | 松籁响起之时 | 5%       | 138.4%   |
| 暴击     | 迪卢克   | 其他       | 狼的末路     | 29.2%    | 50%      |
| 其他     | 达达利亚 | 暴伤       | 飞雷之弦振   | 5%       | 116.2%   |
| 其他     | 达达利亚 | 暴击       | 冬极白星     | 38.1%    | 50%      |
| 其他     | 雷电将军 | 其他       | 薙草之稻光   | 5%       | 50%      |

以迪卢克为例，计算得到的带暴击头和暴伤头的极值点分别为 $(0.484, 1.208)$ 和 $(0.562, 1.052)$ ，调整溢出暴击率后，对其他四件圣遗物暴击率的要求并不高，反而因为太容易超过需要的暴击率数值，暴击伤害还要难堆一点，所以最好带上暴伤头。

最后再补充一点，双暴属性也只是一个乘区，同样也会稀释。在一些情况下，把双暴资源分一些给精通、攻击力或可以转化为攻击力的属性，也许比单纯堆高暴伤收益还要更高。

# 总结

综合前面的所有分析，我们可以得到以下结论：在角色其他乘区数值 $a$ 不变的情况下，

1. 当角色暴击率和暴击伤害总量 $c$ 没有达到一定上限时，角色暴击率和暴击伤害越高，伤害的期望值越高
2. 当角色暴击率和暴击伤害总量 $c$ 保持不变时，角色的暴击率和暴击伤害为 $1:2$ 时，伤害的期望值最高
3. 对于暴击率难以达到极值点的角色，应该佩戴暴击头；对于暴击率较容易达到极值点但是暴击伤害不容易达到极值点的角色，应该佩戴暴伤头

此外，如果不追求期望伤害而追求最大伤害，那么可以适当降低暴击，堆高暴伤。如果考虑深渊buff或者暴击食物，那么保证暴击不溢出即可，其余可全堆暴伤。